分析基础分析框架
Source
Edit
History

如何通过对比得出数据差异？以及什么是二八定律

Catalogue
  1. 1. 写在前面
  2. 2. 对比分析
    1. 2.1. 原理
    2. 2.2. 概念
    3. 2.3. 实例
  3. 3. 帕累托分析
    1. 3.1. 基本概念
    2. 3.2. 实例
  4. 4. 总结

摘要
如何得出数据的差异？如何通过二八定律定位问题的决定性因素？

写在前面

上次学习了数据特征分析中的分布分析，今天继续学习数据特征分析中另外两种分析方法，也就是对比分析以及帕累托分析法。

对比分析

原理

任何事物都既有共性特征，又有个性特征。只有通过对比，才能分辨出事物的性质、变化、发展与别的事物的异同，从而深刻地认识事物的本质和规律。

概念

对比分析通常是把两个互相关系的指标数据进行比较，运用数字展示和说明研究对象规模的大小，水平的高低，速度的快慢，以及各种关系是否协调。

一般有以下几种比较方式：

绝对数比较(相减) / 相对数比较(相除) 结构分析、比例分析、空间比较分析、动态对比分析

实例

1
2
3
4
5
6
# 导入模块

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
1
2
3
4
5
6
# 构建数据

data = pd.DataFrame(np.random.rand(30,2)*1000,
                   columns = ['A_sale','B_sale'],
                   index = pd.period_range('20180801','20180830'))
data.head()
A_sale B_sale
2018-08-01 373.252264 530.096409
2018-08-02 170.119238 288.210134
2018-08-03 755.505567 51.239224
2018-08-04 767.666050 744.299464
2018-08-05 602.851166 676.580069 
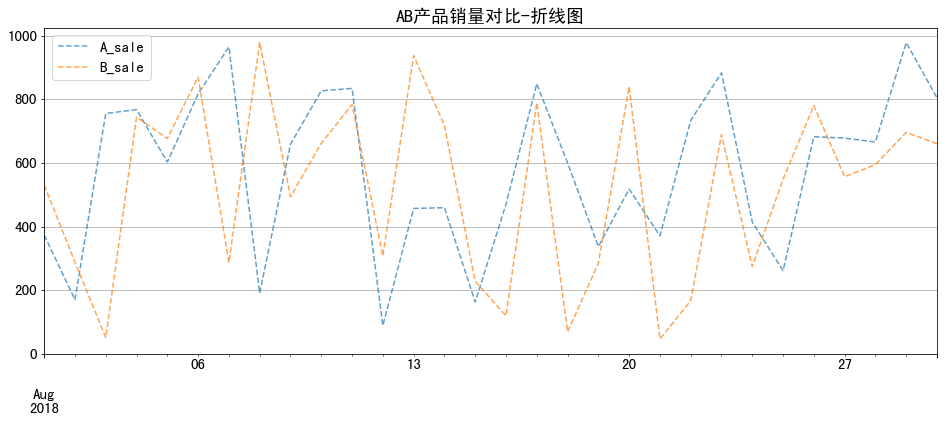
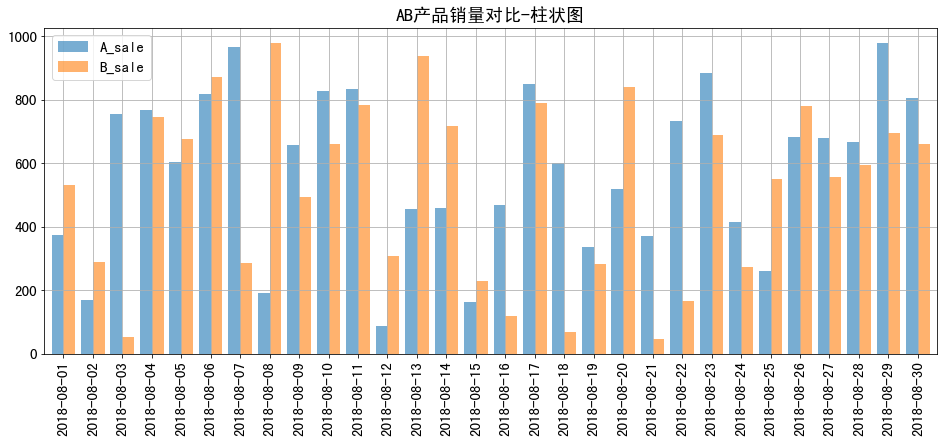
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
plt.rc('font',family = 'simhei',size = 15)
data.plot(kind = 'line',
         style = '--',
         alpha = 0.7,
         figsize = (16,6),
         title = 'AB产品销量对比-折线图',
         grid = True)

# plt.rc('font',family = 'simhei',size = 15)

data.plot(kind = 'bar',
         width = 0.8,
         alpha = 0.6,
         figsize = (16,6),
         title = 'AB产品销量对比-柱状图',
         grid = True)

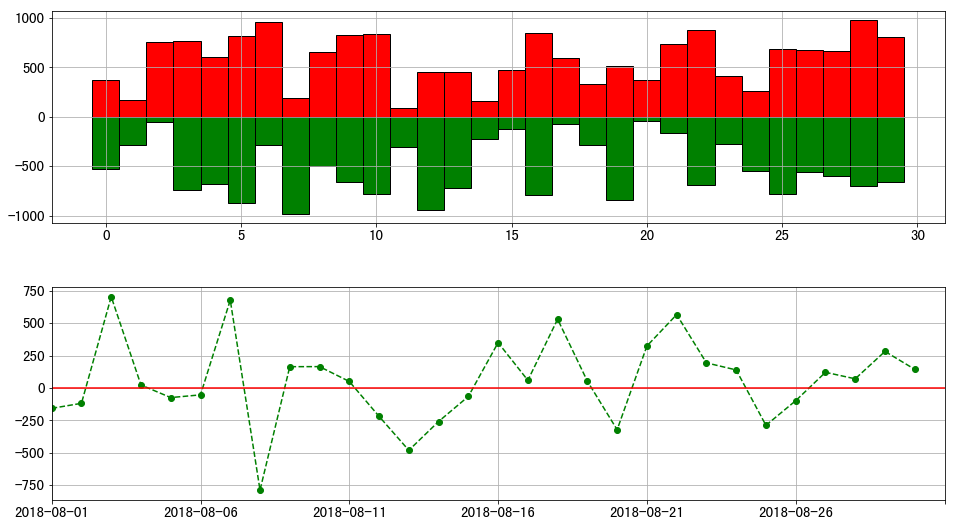
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# 绝对数比较  -  相减

x = range(len(data))
y1 = data['A_sale']
y2 = -data['B_sale']

fig3 = plt.figure(figsize = (16,9))
plt.subplots_adjust(hspace=0.3)

ax1 = fig3.add_subplot(2,1,1)
plt.bar(x,y1,width = 1,facecolor = 'r',edgecolor = 'k')
plt.bar(x,y2,width = 1,facecolor = 'g',edgecolor = 'k')
plt.grid()

ax2 = fig3.add_subplot(2,1,2)
y3 = data['A_sale'] - data['B_sale']
plt.plot(x,y3,'--go')
plt.grid()
plt.xlim(0,len(data))
plt.axhline(0,color = 'r',linestyle = '-')
ax2.set_xticklabels(data.index[::5])


帕累托分析

基本概念

帕累托分析法，是一种得到广泛应用的统计学分析方法。 帕累托分析法应用了“帕累托法则”──关于做20%的事可以产生整个工作80%的效果的法则──通俗地说，柏拉图分析的结果得出百分之八十的后果是由占百分之二十的主要原因造成的，因此帕累托分析法又称二八定律

原因和结果、投入和产出、努力和报酬之间本来就存在着无法解释的不平衡。

一般来说，投入和努力可以分成两种不同类型：多数，他们只能造成少许的影响；少数，他们造成主要的、重大的影响；例如一个公司：80%的利润来自于20%的畅销产品，而其他80%的产品只产生了20%的利润

思路：通过二八原则，去寻找关键的那20%决定性因素

实例

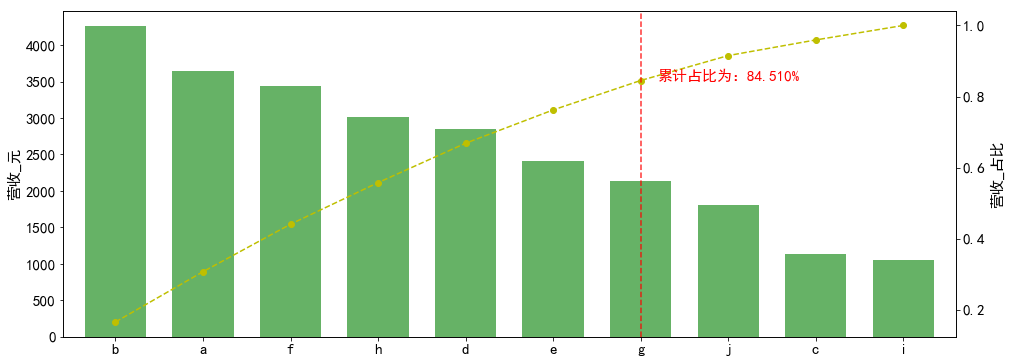
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# 创建数据，10个品类产品的销售额

data = pd.Series(np.random.randn(10)*1200+3000,
                index=list('abcdefghij'))
print(data)
print('---------------------------')

# 对数据进行排序

data.sort_values(ascending = False,inplace = True)

# 营收柱状图

plt.figure(figsize = (16,6))
plt.rc('font',family = 'simhei',size = 15)
data.plot(kind = 'bar',color = 'g',alpha = 0.6,width = 0.7)
plt.ylabel('营收_元')

p = data.cumsum()/data.sum()
key = p[p>0.8].index[0]
key_num = data.index.tolist().index(key)
print('超过80%累计占比的节点值索引为：',key)
print('超过80%累计占比的节点值索引位置为：',key_num)
print('-------------------------')

p.plot(style = '--ko',color = 'y',secondary_y = True)
plt.axvline(key_num,color = 'r',linestyle = '--',alpha = 0.8)
plt.text(key_num+0.2,p[key],'累计占比为：%.3f%%' % (p[key]*100),color = 'r')
plt.ylabel('营收_占比')

key_product = data.loc[:key]
print('核心产品为：')
print(key_product)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
a    3640.475899
b    4259.570101
c    1132.691082
d    2852.087642
e    2411.036428
f    3438.507881
g    2130.585464
h    3009.455301
i    1048.431800
j    1804.076351
dtype: float64
---------------------------
超过80%累计占比的节点值索引为： g
超过80%累计占比的节点值索引位置为： 6
-------------------------
核心产品为：
b    4259.570101
a    3640.475899
f    3438.507881
h    3009.455301
d    2852.087642
e    2411.036428
g    2130.585464
dtype: float64


总结

帕累托分析法也叫主次因素分析法，原先是项目管理中常用的一种方法。它是根据事物在技术和经济方面的主要特征，进行分类排队，分清重点和一般，从而有区别地确定管理方式的一种分的方法。在数据分析中，帕累托分析法可以快速获取数据的各个部分的贡献度，从而制定分析方向与计划。