摘要
什么是正态分布,以及检验数据样本的正态性的方式有哪些?
前言
本文记录学习正态分布以及数据特征的正态性检验。
正态分布
正态分布,又名高斯分布,是一个非常常见的连续概率分布。
定义
正态分布是具有两个参数μ和σ2的连续型随机变量的分布。即若一个随机变量X服从一个数学期望为μ、方差为σ2的正态分布,记为N( μ , σ2 )。
参数μ是服从正态分布的随机变量的均值,参数σ2是此随机变量的方差。
其概率密度函数为正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度,当μ = 0,σ = 1时的正态分布称之为标准正态分布。
特点
- 集中性:正态曲线的高峰位于正中央,即均数所在的位置
- 对称性:正态曲线以均数为中心,左右对称,曲线两端永不于横轴相交
- 均匀变动性:正态曲线由均数所在处开始,分别向左右两侧逐渐均匀下降
- 服从正态分布的随机变量的概率规律为取 μ邻近的值的概率大 ,而取离μ越远的值的概率越小;
- μ决定分布的中心位置
- σ越大,曲线越矮胖,总体分布越分散,反之曲线越瘦高,总体分布越集中
正态性检验
定义
利用观测数据判断总体是否服从正态分布的检验称为正态性检验,是统计判决中重要的一种特殊的拟合优度假设检验
最为基础和常用的正态性检验方法有:
- 直方图初判
- QQ图判断
- K-S检验
直方图检验
1 | # 导入模块 |
1 | # 直方图初判 |
1 | value |
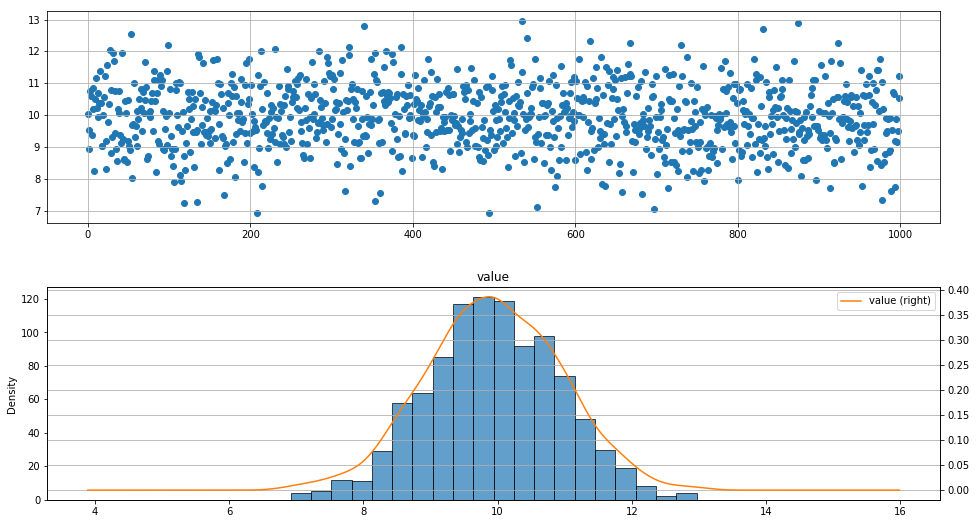
QQ图判断
1 | # QQ图判断 - 通过把测试样本数据的分位数与已知分布相比较,从而来检验数据的分布情况 |
1 | value |
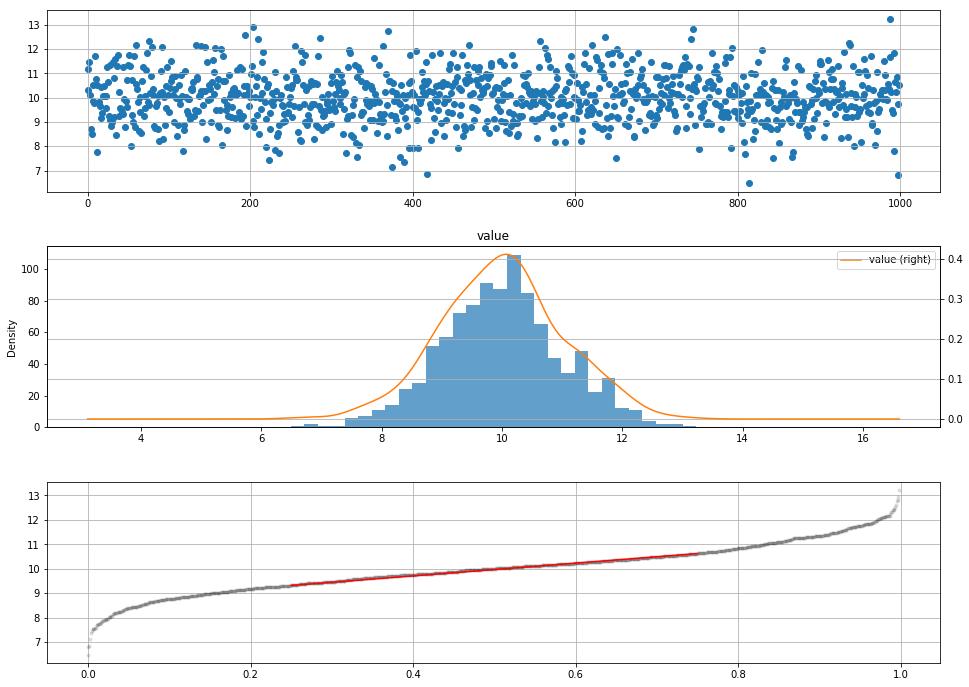
K-S检验
Kolmogorov-Smirnov是比较一个频率分布f(x)与一个理论分布g(x)或者两个观测值分布的检验方法。
以样本数据的累计频数分布与特定的理论分布比较(比如正态分布),如果两者差距小,则推论样本分布取自某特定分布
假设检验问题:
H0:样本的总体分布 服从某特定分布
H1:样本的总体分布 不服从某特定分布
Fn(x):样本的累计分布函数 F0(x):理论分布的分布函数
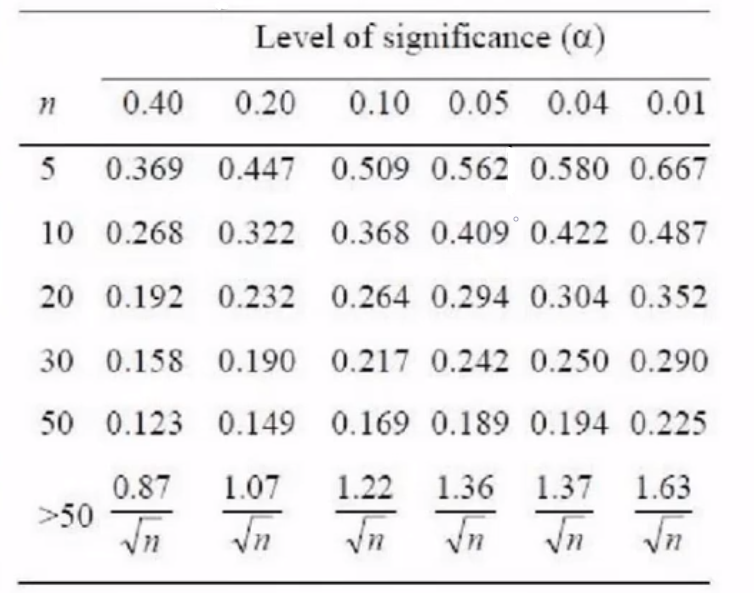
D:F0(x) 与 Fn(x) 差值的绝对值最大值 即 D= max IFn(x) - F0(x)I
D > D( n , α )相比较:p > 0.05则接受H0,p < 0.05则接受H1.
1 | # K - S 检验 → Kolmogorov-Smirnov是比较频率分布f(x)与理论分布g(x)或者两个观测值分布的检验方法 |
1 | 样本均值为:79.74,样本标准差为:5.94 |
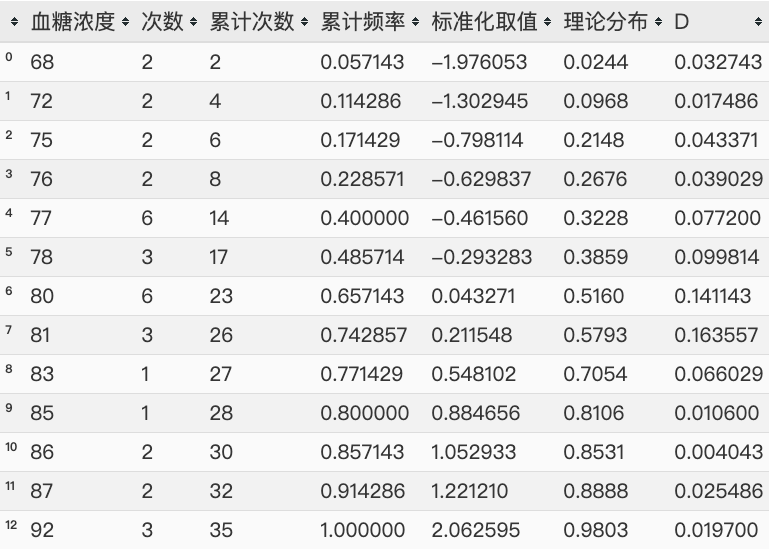
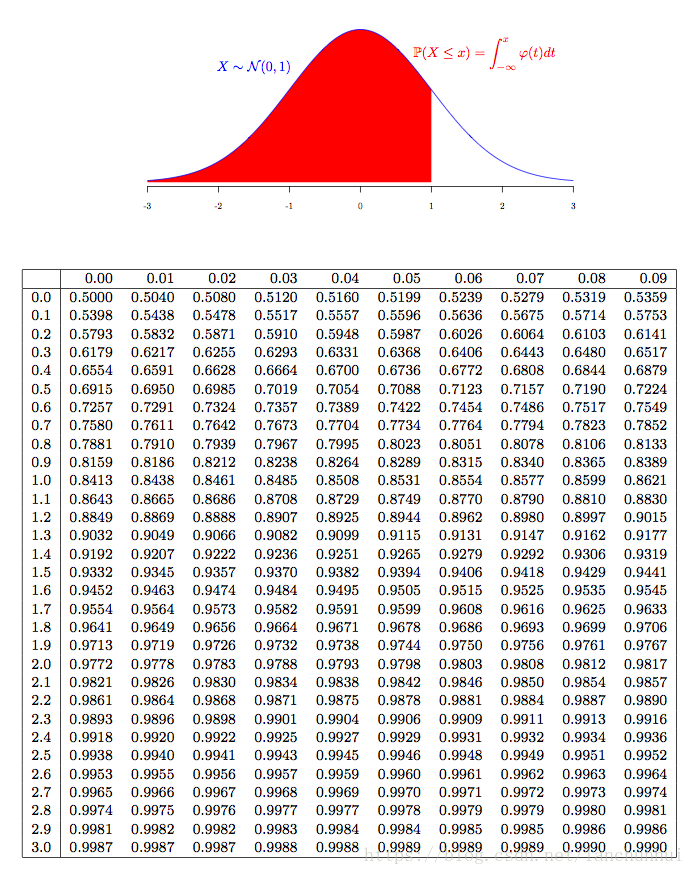
把一个非标准正态分布变成一个标准正态分布----->把非标准正态分布的值变成X = (x-u) /方差----->可以找到理论值。在将这个标准化取值去跟正态分布表去找对应的值。
因为标准化取值的值它本 身就符合正态分布;系统分布与标准分布相减,如果这个函数满足标准正态分布,它的值就应该满足这个表。比如说标准化取值2.064315,其对应的查正态分布表值为0.9803,它的理论分布值是0.9803; 标准化取值-1.9777,去掉负号,查正态分布表为0.9756,正的是0.9756,负的就是1-0.9756=0.0244.可以看到与理论分布值是相对应的。
理论分布就相当于是g(x)就是F0(x),F(n)就是原来的F(n)累计频率。累计频率 - 理论分布 = D
1 | #绘制折线图 |
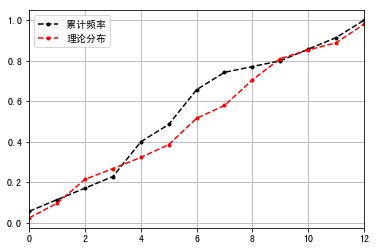
结论:实际观测D值为:0.1597 对应的0.1597放到显著性对照表,我们的样本数据一共35个,在50以内,按0.05的值去算的话,0.1587介于0.158和0.190之间,它所对应的P值是0.2和0.4,这个P值是大于0.05的。 拿到这个D值去那个表里边查,如果大于0.05就说明满足正态分布。
K-S算法
1 | #直接用算法做KS检验 |
1 | KstestResult(statistic=0.1590868892818147, pvalue=0.3061435516448461) |
总结
以上是数据特征分析中的正态分布与正态性检验的全部内容,如有错误,恳请指正,感谢阅读~