摘要
怎样判别数据中的变量是否存在相关性?
得到数据样本又如何进行整理归档?
前言
前面两篇文章列举了数据特征分析中的三种常见的分析方法:分布分析、对比分析和帕累托分析。接下来介绍另外两种分析方法。
相关性分析
在数据特征分析中,研究两个或两个以上随机变量之间相互依存关系的方向和密切程度的方法,就称为相关性分析。而相关性的元素之间需要存在一定的联系或者概率才可以进行相关性分析,所以需要先确定两者之间是否存在相关性。
一般有以下几种方法:
图示处判
-
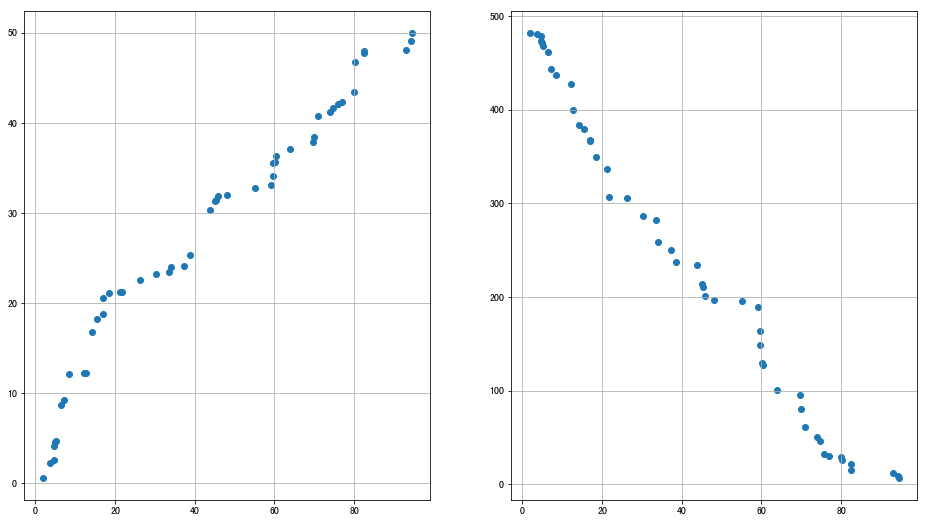
两个变量可以通过线性相关进行分析:
1、k>0:正相关,随着另一个变量的增大而增大;
2、k<0:负相关,随着另一个变量的增大而减小
-
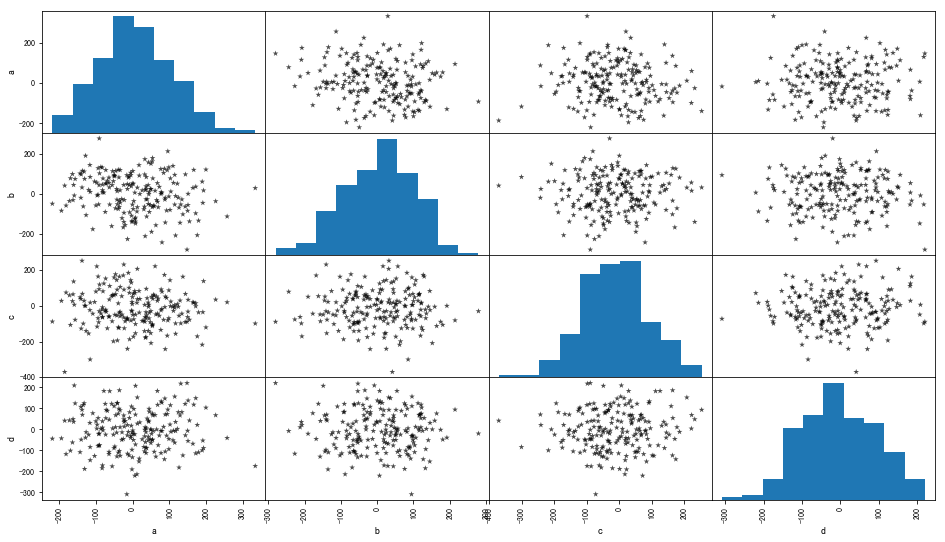
多个变量可以通过散点图矩阵初判多变量之间的关系
1
2
3
4
5
6
|
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
data1 = pd.Series(np.random.rand(50)*100).sort_values()
data2 = pd.Series(np.random.rand(50)*50).sort_values()
data3 = pd.Series(np.random.rand(50)*500).sort_values(ascending = False)
fig = plt.figure(figsize = (16,9))
ax1 = fig.add_subplot(1,2,1)
ax1.scatter(data1,data2)
plt.grid()
ax2 = fig.add_subplot(1,2,2)
ax2.scatter(data1,data3)
plt.grid()
|
1
2
3
4
5
6
7
8
9
10
|
data = pd.DataFrame(np.random.randn(200,4)*100,columns = list('abcd'))
pd.plotting.scatter_matrix(data,figsize = (16,9),
c = 'k',
marker = '*',
diagonal= 'hist',
alpha=0.7,
range_padding=0.1)
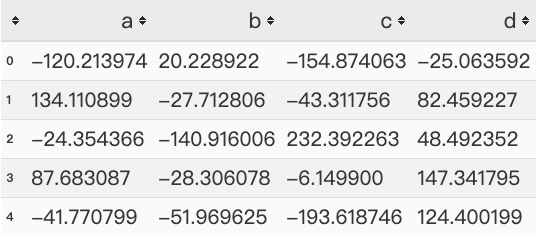
data.head()
|
皮尔逊相关系数
皮尔逊相关系数,又称皮尔逊积矩相关系数是用于度量两个变量X和Y之间的相关(线性相关)
其值介于-1与1之间,o代表无相关性,负值为负相关,正值为正相关
0 < IrI < 1 :表示存在不同程度线性相关
IrI <= 0.3 : 不存在线性相关
0.3 < IrI <= 0.5 : 低度线性相关
0.5 < IrI <= 0.8 : 显著线性相关
IrI > 0.8 : 高度线性相关
tips:前提是数据必须满足正态分布
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
from scipy import stats
data1 = pd.Series(np.random.rand(100)*100).sort_values()
data2 = pd.Series(np.random.rand(100)*50).sort_values()
data = pd.DataFrame({'A':data1.values,'B':data2.values})
print(data.head())
print('------------------------')
jz1,jz2 = data['A'].mean(),data['B'].mean()
bzc1,bzc2 = data['A'].std(),data['B'].std()
print('A正态性检验:\n',stats.kstest(data['A'],'norm',(jz1,bzc1)))
print('B正态性检验:\n',stats.kstest(data['B'],'norm',(jz2,bzc2)))
print('------------------------')
data['(x-jz1)*(y-jz2)'] = (data['A'] - jz1) *(data['B'] - jz2)
data['(x-jz1)**2'] = (data['A'] - jz1) ** 2
data['(y-jz2)**2'] = (data['B'] - jz2) ** 2
print(data.head())
print('------------------------')
r = data['(x-jz1)*(y-jz2)'].sum() / (np.sqrt(data['(x-jz1)**2'].sum() * data['(y-jz2)**2'].sum()))
print('Pearson相关系数为:%.4f' % r)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| A B
0 1.857207 0.487041
1 6.543581 0.498890
2 7.895966 0.650285
3 7.992037 0.837512
4 9.657230 1.412577
------------------------
A正态性检验:
KstestResult(statistic=0.06887931747546477, pvalue=0.7404141658459595)
B正态性检验:
KstestResult(statistic=0.11163895057364082, pvalue=0.1532773076744851)
------------------------
A B (x-jz1)*(y-jz2) (x-jz1)**2 (y-jz2)**2
0 1.857207 0.487041 1219.195525 2588.810639 574.177851
1 6.543581 0.498890 1106.353230 2133.883984 573.610130
2 7.895966 0.650285 1067.174612 2010.768847 566.381190
3 7.992037 0.837512 1056.510686 2002.162152 557.504710
4 9.657230 1.412577 992.418885 1855.915085 530.679045
------------------------
Pearson相关系数为:0.9890
|
Pearson算法
1
2
3
4
5
6
7
8
9
10
11
12
|
data1 = pd.Series(np.random.rand(100)*100).sort_values()
data2 = pd.Series(np.random.rand(100)*50).sort_values()
data = pd.DataFrame({'A':data1.values,'B':data2.values})
print(data.head())
print('------------------------')
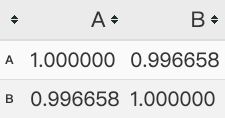
data.corr()
|
1
2
3
4
5
6
7
| A B
0 2.935213 0.097618
1 3.352383 0.774713
2 5.230225 0.846352
3 5.456244 1.010188
4 6.479587 1.077713
------------------------
|
斯皮尔曼相关系数
当数据源不服从正态分布的变量、分类的关联性时,可采用斯皮尔曼相关系数,也称为等级相关系数。
计算逻辑:
对两个变量成对的取值按照从小到大顺序编秩,Rx代表Xi的秩次,Ry代表Yi的秩次
如果两个值大小一样,则秩次为(index1 + index2) / 2
di = Rx - Ry
Sperman系数和Pearson系数在效率上等价
0 < IrI < 1 表示存在不同程度线性相关
IrI <= 0.3 → 不存在线性相关
0.3 < IrI <= 0.5 → 低度线性相关
0.5 < IrI <= 0.8 → 显著线性相关
IrI > 0.8 → 高度线性相关
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
data = pd.DataFrame({'智商':[106,86,100,101,99,103,97,113,112,115],
'每周看电视小时数':[7,0,27,50,12,29,20,28,6,17]})
print(data)
print('----------------------')
data.sort_values('智商',inplace = True)
data['range1'] = np.arange(1,len(data)+1)
data.sort_values('每周看电视小时数',inplace = True)
data['range2'] = np.arange(1,len(data)+1)
print(data)
print('-----------------------')
data['d'] = data['range1'] - data['range2']
data['d2'] = data['d'] ** 2
print(data)
print('-----------------------')
n = len(data)
rs = 1 - 6 * (data['d2'].sum()) / (n * (n**2 - 1))
print('Sperman相关系数为:%.4f' % rs)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| 智商 每周看电视小时数
0 106 7
1 86 0
2 100 27
3 101 50
4 99 12
5 103 29
6 97 20
7 113 28
8 112 6
9 115 17
----------------------
智商 每周看电视小时数 range1 range2
1 86 0 1 1
8 112 6 8 2
0 106 7 7 3
4 99 12 3 4
9 115 17 10 5
6 97 20 2 6
2 100 27 4 7
7 113 28 9 8
5 103 29 6 9
3 101 50 5 10
-----------------------
智商 每周看电视小时数 range1 range2 d d2
1 86 0 1 1 0 0
8 112 6 8 2 6 36
0 106 7 7 3 4 16
4 99 12 3 4 -1 1
9 115 17 10 5 5 25
6 97 20 2 6 -4 16
2 100 27 4 7 -3 9
7 113 28 9 8 1 1
5 103 29 6 9 -3 9
3 101 50 5 10 -5 25
-----------------------
Sperman相关系数为:0.1636
|
Sperman算法
1
2
3
4
5
6
7
8
|
data = pd.DataFrame({'智商':[106,86,100,101,99,103,97,113,112,115],
'每周看电视小时数':[7,0,27,50,12,29,20,28,6,17]})
print(data)
print('----------------------')
data.corr(method = 'spearman')
|
1
2
3
4
5
6
7
8
9
10
11
12
13
| 智商 每周看电视小时数
0 106 7
1 86 0
2 100 27
3 101 50
4 99 12
5 103 29
6 97 20
7 113 28
8 112 6
9 115 17
----------------------
|
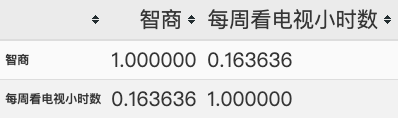
统计分析
统计分析,指对收集到的有关数据资料进行整理归类并进行解释的过程
统计指标对定量数据进行统计描述,常从集中趋势和离中趋势两个方面进行分析
集中趋势
算数平均数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
data = pd.DataFrame({'value':np.random.randint(100,120,100),
'f':np.random.rand(100)})
data['f'] = data['f'] / data['f'].sum()
data.head()
print('-------------')
mean = data['value'].mean()
print('简单算数平均值为:%.2f' % mean)
mean_w = (data['value'] * data['f']).sum() / data['f'].sum()
print('加权算数平均值为:%.2f' % mean_w)
|
1
2
3
| -------------
简单算数平均值为:109.20
加权算数平均值为:109.26
|
位置平均数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
data = pd.DataFrame({'value':np.random.randint(100,130,100),
'f':np.random.rand(100)})
data['f'] = data['f'] / data['f'].sum()
print(data.head())
print('-----------------')
m = data['value'].mode().tolist()
print('众数为' % m)
med = data['value'].median()
print('中位数为%i' % med)
plt.rc('font',family = 'simhei',size = 15)
plt.figure(figsize = (16,6))
data['value'].plot(kind = 'kde',style = '--k',grid = True)
plt.axvline(mean,color = 'r',linestyle = '--',alpha = 0.6)
plt.text(mean + 5,0.005,'简单算数平均值为:%.2f' % mean,color = 'r')
plt.axvline(mean_w,color = 'b',linestyle = '--',alpha = 0.6)
plt.text(mean + 5,0.01,'加权算数平均值为:%.2f' % mean_w,color = 'b')
plt.axvline(med,color = 'g',linestyle = '--',alpha = 0.6)
plt.text(med + 5,0.015,'简单算数平均值为:%.2f' % med,color = 'g')
|
1
2
3
4
5
6
7
8
9
| value f
0 105 0.002597
1 118 0.000580
2 122 0.004448
3 122 0.005803
4 104 0.000088
-----------------
众数为
中位数为116
|
1
| Text(121.0, 0.015, '简单算数平均值为:116.00')
|
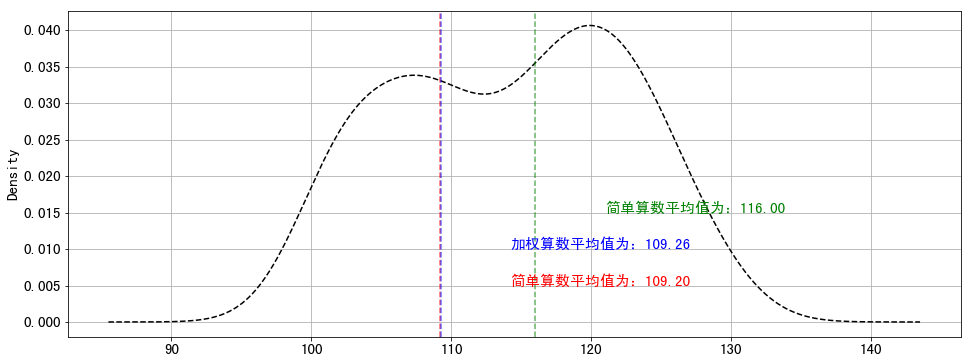
离中趋势
极差与分位差
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
data = pd.DataFrame(np.random.rand(30,2)*1000,
columns = ['A_sale','B_sale'],
index = pd.period_range('20180801','20180830'))
print(data.head())
print('---------------')
a_r = data['A_sale'].max() - data['A_sale'].min()
b_r = data['B_sale'].max() - data['B_sale'].min()
print('A销售额的极差为:%.2f,B销售额的极差为:%.2f' % (a_r,b_r))
print('---------------')
sta = data['A_sale'].describe()
stb = data['B_sale'].describe()
a_iqr = sta.loc['75%'] - sta.loc['25%']
b_iqr = stb.loc['75%'] - stb.loc['25%']
print('A销售额的分位差为:%.2f,B销售额的分位差为:%.2f' % (a_iqr,b_iqr))
print('---------------')
color = dict(boxes = 'Green',whiskers = 'Orange',medians = 'Blue',
caps = 'Gray')
data.plot.box(vert = False,grid = True,color = color,figsize = (16,8))
plt.xlim(0,1000)
|
1
2
3
4
5
6
7
8
9
10
11
| A_sale B_sale
2018-08-01 284.722111 866.702850
2018-08-02 443.579648 448.190161
2018-08-03 365.901111 680.083981
2018-08-04 87.793742 984.790348
2018-08-05 544.437922 90.517866
---------------
A销售额的极差为:954.10,B销售额的极差为:953.65
---------------
A销售额的分位差为:455.72,B销售额的分位差为:637.73
---------------
|
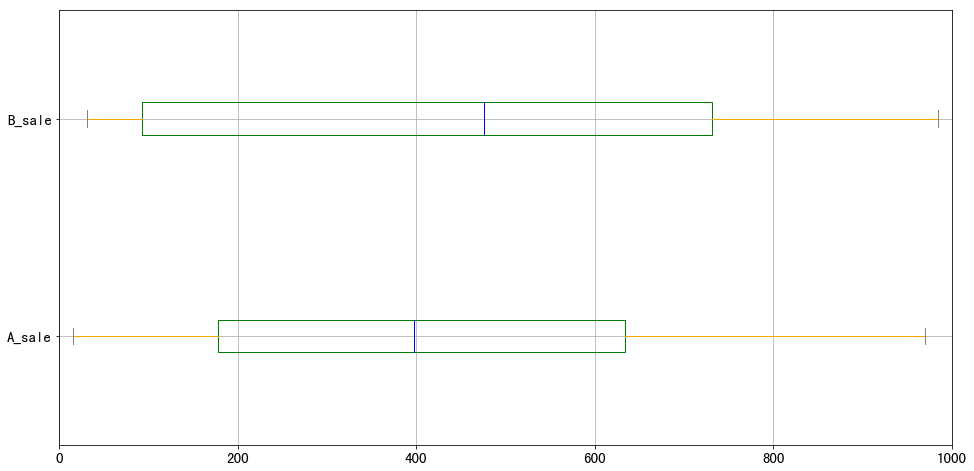
方差与标准差
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
a_std = sta.loc['std']
b_std = stb.loc['std']
a_var = data['A_sale'].var()
b_var = data['B_sale'].var()
print('A销售额的标准差为:%.2f,B销售额的标准差为:%.2f' % (a_std,b_std))
print('A销售额的方差为:%.2f,B销售额的方差为:%.2f' % (a_var,b_var))
fig = plt.figure(figsize = (16,6))
ax1 = fig.add_subplot(1,2,1)
data['A_sale'].plot(kind = 'kde',style = 'k--',grid = True,title = 'A密度曲线')
plt.axvline(sta.loc['50%'],color = 'r',linestyle = '--', alpha = 0.6)
plt.axvline(sta.loc['50%']-a_std,color = 'b',linestyle = '--', alpha = 0.6)
plt.axvline(sta.loc['50%']+a_std,color = 'b',linestyle = '--', alpha = 0.6)
ax2 = fig.add_subplot(1,2,2)
data['B_sale'].plot(kind = 'kde',style = 'k--',grid = True,title = 'B密度曲线')
plt.axvline(stb.loc['50%'],color = 'r',linestyle = '--', alpha = 0.6)
plt.axvline(stb.loc['50%']-b_std,color = 'b',linestyle = '--', alpha = 0.6)
plt.axvline(stb.loc['50%']+b_std,color = 'b',linestyle = '--', alpha = 0.6)
|
1
2
| A销售额的标准差为:270.43,B销售额的标准差为:315.20
A销售额的方差为:73133.58,B销售额的方差为:99350.72
|
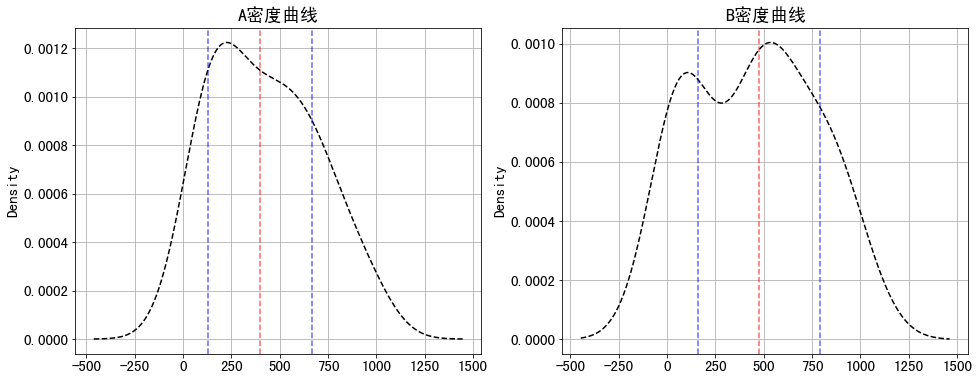
总结
数据特征分析的几个基本分析思维已学习完,分别有:分布分析、对比分析、帕累托分析、相关性分析以及统计分析。这五种分析思路是对数据特征进行分析的基础,可以引导自己快速将数据整理归类,记录下来以供随时翻阅,感谢阅读~







