分析基础算法
Source
Edit
History

随机算法之蒙特卡罗

Catalogue
  1. 1. 随机算法
    1. 1.1. 蒙特卡罗算法
      1. 1.1.1. π的计算
      2. 1.1.2. 积分计算
      3. 1.1.3. 实例
  2. 2. 写在结尾

摘要
随机算法的基础认知以及简单推导应用～

随机算法

蒙特卡罗算法

蒙特卡罗算法，又称随机抽样或统计实验方法,是以概率和统计理论方法为基础的一种计算方法

使用随机数(或更常见的伪随机数)来解决很多计算问题,将所求解的问题同一定的概率模型向联系,用电子计算机实现统计模拟或抽样,以获得问题的近似解

以一个概率模型为基础,按照这个模型所描绘段得过程,通过模拟实验的结果,作为问题的近似解
1、构造或描述概率过程
2、实现从已知概率分布抽样
3、建立各种估计量

优点：简单快速
特点：随机采样上计算得到近似结果,随着采样的增多,得到的结果是正确结果的概率逐渐加大

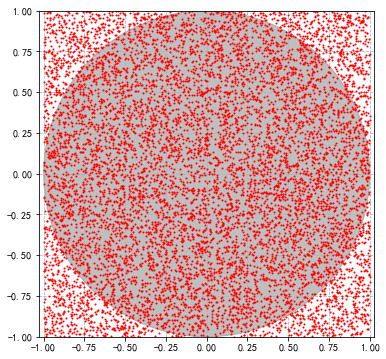
π的计算

1
2
3
4
5
6
#导入模块

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
# 设置投点次数
n = 10000

# 设置半径
r = 1.0

# 圆心
a,b = (0.0,0.0)

#区域边界

xmin,xmax = a-r,a+r
ymin,ymax = b-r,b+r

# 在正方形区域内随机投点

# numpy.random.uniform(low,high,size) → 从一个均匀分布[low,high)中随机采样，均匀分布

x = np.random.uniform(xmin,xmax,n)
y = np.random.uniform(ymin,ymax,n)

fig = plt.figure(figsize = (6,6))
axes = fig.add_subplot(1,1,1)
plt.plot(x,y,'ro',markersize = 1)
plt.axis('equal')
plt.xlim(-1,1)
plt.ylim(-1,1)

d = np.sqrt((x - a)**2 + (y - b)**2)
res = sum(np.where(d<r,1,0))
pi = 4 * res / n
print(pi)

# 导入绘制圆形 Circle (椭圆Ellipse)

from matplotlib.patches import Circle

circle = Circle(xy = (a,b),radius = r,alpha = 0.5,color = 'gray')
axes.add_patch(circle)
plt.grid(True,linestyle = '--',linewidth = '0.8')
plt.show()
1
3.1256

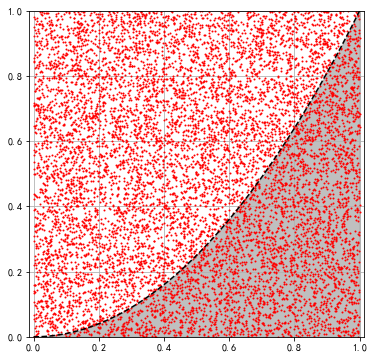
积分计算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#  设置投点次数
n = 10000

# 矩形区域边界
x_min,x_max = 0.0,1.0
y_min,y_max = 0.0,1.0

#在矩形区域内随机投点

x = np.random.uniform(x_min,x_max,n)
y = np.random.uniform(y_min,y_max,n)

#统计落在函数图像下方的点的数目

def f(x):
    return x**2

res = sum(np.where(y < f(x),1,0))

#计算定积分的近似值

integral = res / n
print('integral:',integral)

fig = plt.figure(figsize = (6,6))
axes = fig.add_subplot(111)
axes.plot(x,y,'ro',markersize = 1)
plt.axis('equal')
plt.xlim(0,1)
plt.ylim(0,1)

xi = np.linspace(0,1,100)
yi = xi ** 2
plt.plot(xi,yi,'--k')
plt.fill_between(xi,yi,0,color = 'gray',alpha = 0.5,label = 'area')
plt.grid()
1
integral: 0.3367

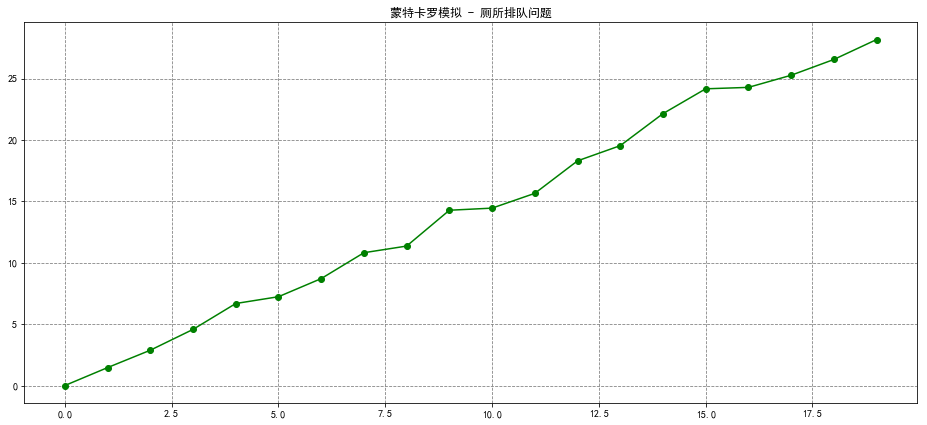
实例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
# 厕所排队问题

# 1、两场电影结束时间相隔较长,互不影响
# 2、每场电影结束之后会有20个人想上厕所
# 3、这20个人会在0到10分钟内全部到达厕所
# 4、每个人上厕所时间在1-3分钟之间

# 首先模拟最简单的情况,也就是厕所只有一个位置,不考虑俩人共用的情况则没人必须等上一人完毕方可进行

# 参数：到达时间 / 等待时间 / 开始上厕所时间 / 结束时间

arrivingtime = np.random.uniform(0,10,size = 20)
arrivingtime.sort()
workingtime = np.random.uniform(1,3,size = 20)
# np.random.uniform 随机数：均匀分布的样本值
print(arrivingtime)
print('--------------------------')

startingtime = [0 for i in range(20)]
finishtime = [0 for i in range(20)]
waitingtime = [0 for i in range(20)]
emptytime = [0 for i in range(20)]

startingtime[0] = arrivingtime[0]
finishtime[0] = startingtime[0] + workingtime[0]
waitingtime[0] = startingtime[0] - arrivingtime[0]

print(startingtime[0],workingtime[0],finishtime[0],waitingtime[0])
print('---------------------------')

# 判断：如果下一个人在上一个人完成之前到达,则 开始时间 = 上一个人的结束时间
# 否则：开始时间 = 到达时间,且存在空闲时间 = 到达时间 - 上一个人的完成时间

for i in range(1,len(arrivingtime)):
    if finishtime[i-1] > arrivingtime[i]:
        startingtime[i] = finishtime[i-1]
    else:
        startingtime[i] = arrivingtime[i]
        emptytime[i] = arrivingtime[i] - finishtime[i-1]
    finishtime[i] = startingtime[i] + workingtime[i-1]
    waitingtime[i] = startingtime[i] - arrivingtime[i]
    print('第%d个人：到达时间 开始时间 "工作"时间 完成时间 等待时间\n' % i,
         arrivingtime[i],
         startingtime[i],
         workingtime[i],
         finishtime[i],
         waitingtime[i],
         '\n')
print('arerage waiting time is %f' % np.mean(waitingtime))
print('-----------------------------')
    
fig = plt.figure(figsize = (16,7))
plt.plot(waitingtime,'-go')
plt.grid(True,linestyle = '--',color = 'gray',linewidth = '0.8')
plt.title('蒙特卡罗模拟 - 厕所排队问题')
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
[0.16587897 0.62204463 1.12297214 1.61646409 2.2734175  3.58188608
 4.06180627 4.42582219 4.92397497 5.00023146 6.3967079  6.82771899
 6.96481151 7.21465387 7.34371744 7.51496538 8.68568567 8.94934034
 9.61589877 9.7940074 ]
--------------------------
0.16587897242361538 1.9163595239913254 2.0822384964149405 0.0
---------------------------
第1个人：到达时间 开始时间 "工作"时间 完成时间 等待时间
 0.6220446336305152 2.0822384964149405 2.188198872364582 3.998598020406266 1.4601938627844253 

第2个人：到达时间 开始时间 "工作"时间 完成时间 等待时间
 1.122972137882483 3.998598020406266 2.764457045410645 6.1867968927708485 2.875625882523783 

第3个人：到达时间 开始时间 "工作"时间 完成时间 等待时间
 1.6164640948717424 6.1867968927708485 1.8619334107218273 8.951253938181495 4.570332797899106 

第4个人：到达时间 开始时间 "工作"时间 完成时间 等待时间
 2.27341749721095 8.951253938181495 1.9558472451168596 10.813187348903321 6.677836440970545 

第5个人：到达时间 开始时间 "工作"时间 完成时间 等待时间
 3.5818860753684123 10.813187348903321 2.4715009771412073 12.76903459402018 7.231301273534909 

第6个人：到达时间 开始时间 "工作"时间 完成时间 等待时间
 4.061806266415359 12.76903459402018 1.0395021167184366 15.240535571161388 8.70722832760482 

第7个人：到达时间 开始时间 "工作"时间 完成时间 等待时间
 4.425822187022732 15.240535571161388 2.9938063833706754 16.280037687879826 10.814713384138656 

第8个人：到达时间 开始时间 "工作"时间 完成时间 等待时间
 4.923974971103213 16.280037687879826 1.5688516924561942 19.2738440712505 11.356062716776613 

第9个人：到达时间 开始时间 "工作"时间 完成时间 等待时间
 5.0002314565754515 19.2738440712505 1.6350976155013934 20.842695763706693 14.273612614675049 

第10个人：到达时间 开始时间 "工作"时间 完成时间 等待时间
 6.396707898323078 20.842695763706693 2.78313954407255 22.477793379208087 14.445987865383614 

第11个人：到达时间 开始时间 "工作"时间 完成时间 等待时间
 6.827718993543048 22.477793379208087 1.4873508450792379 25.260932923280638 15.65007438566504 

第12个人：到达时间 开始时间 "工作"时间 完成时间 等待时间
 6.96481151330325 25.260932923280638 2.7352000597223616 26.748283768359876 18.29612140997739 

第13个人：到达时间 开始时间 "工作"时间 完成时间 等待时间
 7.21465386868163 26.748283768359876 2.1947890646530044 29.48348382808224 19.533629899678246 

第14个人：到达时间 开始时间 "工作"时间 完成时间 等待时间
 7.3437174368142575 29.48348382808224 1.2871138118247274 31.678272892735244 22.139766391267983 

第15个人：到达时间 开始时间 "工作"时间 完成时间 等待时间
 7.514965384306672 31.678272892735244 1.2507700564206545 32.96538670455997 24.163307508428574 

第16个人：到达时间 开始时间 "工作"时间 完成时间 等待时间
 8.685685670740416 32.96538670455997 1.9506767657028061 34.216156760980624 24.279701033819553 

第17个人：到达时间 开始时间 "工作"时间 完成时间 等待时间
 8.949340336055485 34.216156760980624 1.8000774818307035 36.16683352668343 25.26681642492514 

第18个人：到达时间 开始时间 "工作"时间 完成时间 等待时间
 9.615898768155551 36.16683352668343 1.1238441426072674 37.96691100851414 26.55093475852788 

第19个人：到达时间 开始时间 "工作"时间 完成时间 等待时间
 9.794007397518186 37.96691100851414 1.6867760138470005 39.09075515112141 28.172903610995952 

arerage waiting time is 14.323308
-----------------------------

写在结尾

以上是对随机算法中的蒙特卡罗算法的一些初步认知。在数据分析中，这种随机算法应用的十分广泛，也是初学者必知必会，有任何不对的地方，恳请指正～感谢阅读！